3983. Mancunian and colored tree

After a busy week at work, the residents of Manchester and Liverpool decided to go on a hike for the weekend. While walking through the forest, they came across a unique tree consisting of n vertices. The vertices of the tree are numbered from 1 to n.

Each vertex of the tree is assigned one of c possible colors. To fight boredom, they decided to test their logical skills. The root of the tree is vertex 1. For each vertex, they decided to find the nearest ancestor whose color matches the color of that vertex.

Input. The first line contains two integers n and c (1 ≤ n, c ≤ 10⁵) – the number of vertices in the tree and the number of possible colors.

The second line contains n – 1 integers, where the i-th number indicates the parent of the (i + 1)-th vertex.

The third line contains n integers representing the colors of the vertices. The color values range from 1 to c inclusive.

Output. Print a single line with n numbers, where the i-th number is the vertex that is the nearest ancestor of the i-th vertex with the same color. If such an ancestor does not exist for a vertex, print -1.

Sample input	Sample output
5 4 1 1 3 3 1 4 2 1 2	-1 -1 -1 1 3

SOLUTION

graphs, depth first search

Algorithm analysis

Consider a simpler version of the problem. Let all the vertices of the tree be painted with one color. Declare a stack, that is empty initially. Run depth first search from the root of the tree. While entering the vertex v, put it into the stack. At the end of processing vertex v, remove the top of the stack (this will be the vertex v). When the depth search is complete, the stack will be empty.

Question: what will be on the top of the stack when you enter the vertex v and before you put v on the stack?

Now let’s solve our problem. Create c stacks, one for each color (for example, a vector of stacks). Initially, all stacks are empty. Start the depth-first search from the root, from the vertex 1. Processing the vertex v of color color consists of the following steps:

· If stack s[color] is not empty, then its top contains the vertex that is the closest ancestor of v, which has the same color as v. If stack is empty, then the required vertex does not exist, the answer for v will be -1.

· Push vertex v into stack s[color].

· Run depth first search from all sons of the vertex v.

· Pop the vertex from the stack s[color].

When during the depth-first search we are in the vertex v, the stacks store information about the colors of all vertices located on a single path from the root to v. That is, stack s[color] contains the vertex numbers on the path from the root to v, that has the color color. The vertices are pushed onto the stack in the order they are visited by DFS.

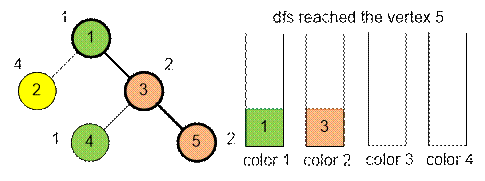
Example

When depth-first search reaches the vertex 5, out of c = 4 stacks, two will be empty (corresponding to colors 3 and 4). Stack number 1 (first color) contains vertex 1, stack number 2 (second color) contains vertex 3. Vertex number 5 has color 2, therefore the closest ancestor with the same color will be the vertex located at the top of stack 2. This ancestor for the vertex 5 will be the vertex 3.

Algorithm realization

Declare the arrays.

vector<int> col, res;

vector<vector<int> > g;

vector<stack<int> > s;

Function dfs runs the depth first search from the vertex v.

void dfs(int v)

{

Vertex v has color color.

int color = col[v];

Store in res[v] the number of the lowest ancestor of the node v that has color color.

if(s[color].empty())

res[v] = -1;

else

res[v] = s[color].top();

Push the vertex v onto the stack number color.

s[color].push(v);

Iterate over the sons to of the vertex v and run recursively the depth-first search from them.

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

dfs(to);

}

The depth first search exits from the vertex v. Pop v from the stack number color.

s[color].pop();

}

The main part of the program. Read the input data. Construct a tree.

scanf("%d %d",&n,&c);

g.resize(n+1);

for(i = 2; i <= n; i++)

{

scanf("%d",&val);

g[val].push_back(i);

}

Read the colors of the tree vertices.

col.resize(n+1);

for(i = 1; i <= n; i++)

scanf("%d",&col[i]);

Run the depth first search from the vertex 1.

s.resize(c+1);

res.resize(n+1);

dfs(1);

Print the answer.

for(i = 1; i <= n; i++)

printf("%d ",res[i]);

printf("\n");